[Algorithm] Tree

트리(Tree)

데이터를 표현할 때 선형만으로는 표현하기 어려운 구조도 많다.
대표적으로 계층 구조가 있는데, 이 계층 구조를 표현하기 위한 자료구조가 트리(Tree)이다.

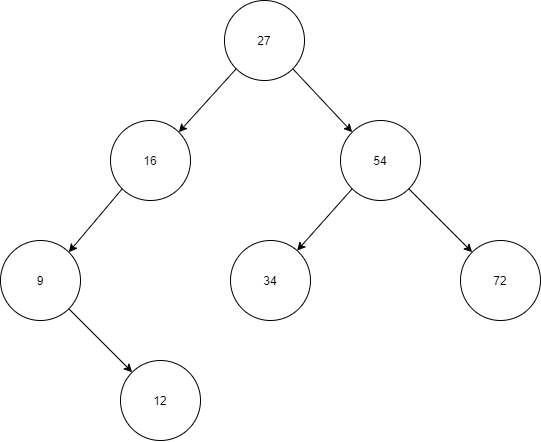
트리의 구성 요소

• 연결된 두 노드 중에 상위 노드를 부모 노드(Parent Node), 하위 노드를 자식 노드(Child Node)라고 한다.
• 부모가 같은 노드들을 형제 노드(Sibling Node)라고 한다.
• 부모 노드와 그 부모들을 모두 통틀어 선조 노드(Ancestor Node)라고 한다.
• 자식 노드와 그 자식들을 모두 통틀어 자손 노드(Descendant Node)라고 한다.
• 다른 모든 노드들을 자손으로 갖는 노드를 루트 노드(Root Node)라고 한다.

트리의 속성

• 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수를 깊이라고 하며, 트리에서 가장 긴 깊이를 높이라고 한다.
• 트리는 재귀적인 속성을 갖는다. 트리의 각 노드에서 해당 노드와 그 자손들을 모두 모으면 그 또한 하나의 트리이며 서브 트리라고 한다.

• 트리의 표현에 있어 일반적인 형태는 각 노드를 하나의 구조체 또는 객체로 표현하고, 이들을 서로 포인터로 연결하여 표현한다.

    typedef struct __TreeNode{
        int value;
        TreeNode * parent;
        vector<TreeNode*> children;
    } TreeNode;
  

트리의 순회

트리의 모든 데이터를 순회하기 위해서는 재귀적 특성을 이용한다.
트리의 루트를 방문한 뒤 각 서브트리를 재귀적으로 방문하는 방식으로 모든 노드에 접근할 수 있다.

void printTree(TreeNode * root){
	cout << root->value << endl;

	for(int i = 0 ; i < root->children.size() ; i++){
		printTree(root->children[i]);
	}
}

트리의 높이를 구할 때도 재귀적 특성을 이용한 순회를 사용한다.

int height(TreeNode * root){
	int height = 0;

	for(int i = 0 ; i < root->children.size() ; i++){
		height = max(height, 1 + height(root->children[i]));
	}

	return height;
}

이진 트리와 순회

이진 트리란 각 노드가 왼쪽과 오른쪽에 최대 하나의 자식을 가지는 구조이다.

typedef struct __TreeNode{
	int value;
	TreeNode * left;
	TreeNode * right;
} TreeNode;

이진 트리의 순회에서는 루트 노드를 언제 방문하는지에 따라 세 가지로 나눠진다.

1. PreOrder(전위 순회) : ‘루트 노드 > 좌측 트리 > 우측 트리’ 순으로 방문

    // 방문 순서 : 27, 16, 9 12, 54, 36, 72	
    void preOrder(TreeNode * node){
        cout << node->value;
        if(node->left != nullptr) preOrder(node->left);
        if(node->right != nullptr) preOrder(node->right);
    }
   

2. InOrder(중위 순회) : ‘좌측 트리 > 루트 노드 > 우측 트리’ 순으로 방문

    // 방문 순서 : 9, 12, 16, 27, 36, 72
    void inOrder(TreeNode * node){
        if(node->left != nullptr) inOrder(node->left);
        cout << node->value;
        if(node->right != nullptr) inOrder(node->right);
    }
   

3. PostOrder(후위 순회) : ‘좌측 트리 > 우측 트리 > 루트 노드>’ 순으로 방문

    // 방문 순서 : 12, 9, 16, 36, 72, 54, 27
    void postOrder(TreeNode * node){
        if(node->left != nullptr) postOrder(node->left);
        if(node->right != nullptr) postOrder(node->right);
        cout << node->value;
    }
   

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략