[Algorithm] 부분 합 구하기

부분합

어떤 배열에서 a번에서 b번까지의 합을 구할 필요가 있다고 하면, 다음과 같이 쉽게 구현 가능하다.

int rangeSum(const vector<int> & arr, int a, int b){
	int sum = 0;
	for(int i = a ; i <= b ; i++) sum += arr[i];
	
	return sum;
}

하지만 구해야할 (a, b) 쌍이 여러 개라면 각 케이스마다 $O(N)$이 걸리는 것은 효율이 좋지 않다.
이를 상수 시간안에 처리하기 위해 부분합 배열을 사용한다.

i	0	1	2	3	4	5	6
arr	100	97	86	79	66	52	49
psum	100	197	283	362	428	480	529

(a, b)의 합은 $psum[b] - psum[a-1]$으로 표현될 수 있으며 $O(1)$에 구할 수 있다.

vector<int> partialSum(const vector<int> & arr){
	vector<int> ret(arr.size());
	ret[0] = arr[0];
	for(int i = 1 ; i < ret.size() ; i++){
		ret[i] = ret[i-1] + arr[i];
	}

	return ret;
}

// a ~ b를 구함
int rangeSum(const vector<int> & psum, int a, int b){
	if(a == 0) return psum[b];
	else return psum[b] - psum[a-1];
}

2차원 배열의 부분합

2차원 배열에서도 부분합을 정의할 수 있다.

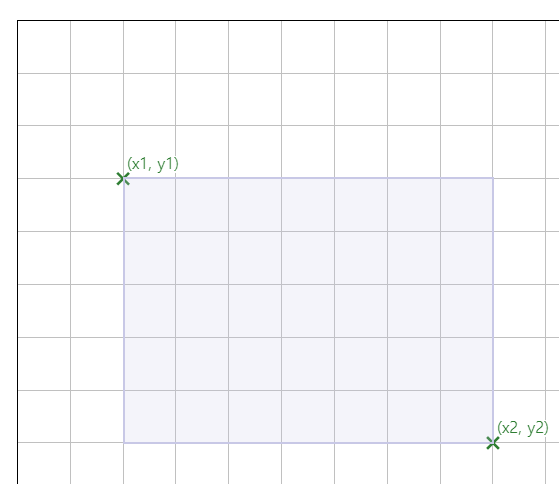
그림과 같이 (x1, y1)에서 (x2, y2)에 이르는 합을 구하기 위해서는 다음과 같은 식을 세울 수 있다.

$ sum = psum[x_2, y_2] - psum[x_1-1, y_2] - psum[x_2, y_1-1] + psum[x_1-1, y_1-1] $

vector<vector<int> > partialSum_2d(const vector<vector<int> > arr){
	vector<vector<int> > ret(arr.size(), vector<int>(arr[0].size(), 0));

	ret[0][0] = arr[0][0];
	for(int i = 1 ; i < ret.size() ; i++) ret[i][0] = ret[i-1][0] + arr[i][0];
	for(int i = 1 ; i < ret[0].size() ; i++) ret[0][i] = ret[0][i-1] + arr[0][i];

	for(int i = 1 ; i < ret.size() ; i++){
		for(int j = 1 ; j < ret[i].size() ; j++){
		ret[i][j] = ret[i-1][j] + ret[i][j-1] - ret[i-1][j-1] + arr[i][j]; 
		}
	}
	
	return ret;
}

int gridSum(const vector<vector<int> > & psum, int x1, int y1, int x2, int y2){
	int ret = psum[y2][x2];

	if(y1 > 0) ret -= psum[y1-1][x2];
	if(x1 > 0) ret -= psum[y2][x1-1];
	if(y1 > 0 && x1 > 0) ret += psum[y1-1][x1-1];

	return ret;
}

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략