[Algorithm] 네트워크 유량

Network Flow

그래프에 있어 정점 간의 길이 말고도 중요한 개념인 ‘용량’이 있다. 예를들어 네트워크를 통해 파일을 받는다고 했을 때 중요한 것은 패킷이 최단 경로로 가는것이 아니라 한 번에 얼마나 많은 용량을 밀어 넣을 수 있는 것이 중요하다.

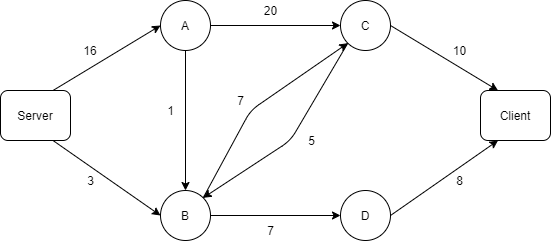
단일 경로로 보냈을 때는 경로에 속한 간선 중 가장 작은 것에 의존적이다. 예를 들어 a, c를 통해 내보낸다고 하면 전송은 초당 10이다.

하지만 경로를 쪼개서 보낸다고 가정하면

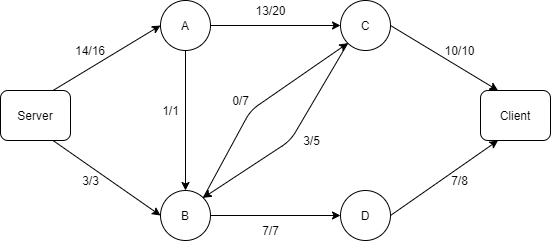
‘매번 지나가는 양 / 간선의 용량’으로 표현했을 때 위와 같이 구성하면 클라이언트에 초당 17의 데이터가 들어간다.

이렇게 그래프에서 용량이 존재할 때 두 정점 사이에서 얼마나 많은 Flow가 발생할 수 있는지 계산하는 문제를 Network Flow라고 부른다.

용어 및 개념

Flow Network란 그래프의 각 간선에 capacity 개념이 존재하는 방향 그래프를 의미한다.

Network flow에서는 플로우가 시작되는 Source Vertex, 플로우가 도착하는 Sink Vertex 두 개의 특수한 정점이 존재한다. 그리고 용량을 c, 유량을 f로 표현했을 때 아래 속성들을 만족한다.

1. $ f(u, v) \leq c(u, v) $
   용량 제한 속성. 각 간선의 유량은 용량을 초과할 수 없다.

2. $ f(u, v) = -f(v, u) $
   유량 대칭성. u에서 v로 흘러올 경우, v 입장에서는 u로 음수의 유량을 보내는 것으로 생각한다.

3. $ \sum_{v \in V} f(u, v) = 0 $
   유량 보존. 각 정점으로 들어오는 플로우와 나가는 플로우의 양의 합은 같아야 한다.

Ford-Fulkerson Algorithm

유량 문제를 해결하는 방법으로 포드-풀커슨 알고리즘이 존재한다. 모든 간선의 flow를 0으로 설정하고, source에서 sink로 보낼 수 있는 경로를 찾는 것을 반복하는 방식이다.

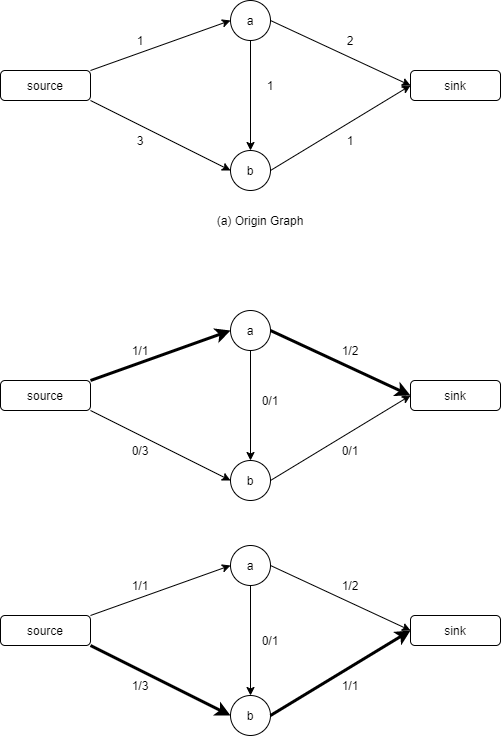
그런데 단순한 설명으로는 어떤 경로를 탐색하느냐에 따라 결과가 달라진다.

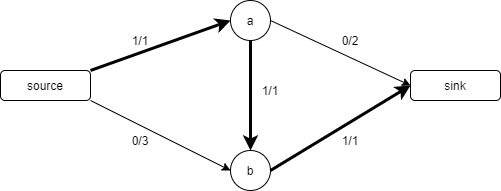
이를 해결하기 위해 먼저 u에서 v로 보낼 수 있는 잔여 용량을 간선의 전체 용량에서 현재 플로우를 뺀 값이라고 정의하자.

$ r(u, v) = c(u, v) - f(u, v) $

그리고 유량 대칭성을 이용하여 해결할 수 있다. $ f(u, v) = -f(v, u) $ 인 점을 이용하면 $ f(b, a) = -1 $이 성립한다. $ r(b, a) = 0 - (-1) = 1 $ 이 성립하므로 b에서 a로 1의 유량을 보낼 수 있음을 식이 나타낸다. b에서 a로 연결된 간선은 없지만 b에서 a로 유량을 보내는 것을 a에서 b로 들어오는 유량을 막음으로써 구현 가능 한 것이다.

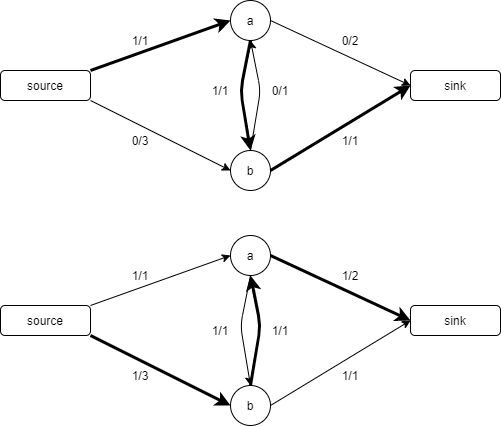
이렇게 되면 위의 케이스에서 어떤 경로를 선택하든 최대 유량을 구할 수 있다.

구현

#define INF 99999999
#define MAX_V 30

#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

int V;
int capacity[MAX_V][MAX_V];
int flow[MAX_V][MAX_V];

int networkFlow(int, int);

int main(){
	V = 4;

	capacity[0][1] = 1;
	capacity[0][2] = 2;
	
	capacity[1][2] = 1;
	capacity[1][3] = 3;

	capacity[2][3] = 1;

	int totalFlow = networkFlow(0, 3);
	cout << totalFlow << endl;

	return 0;
}

int networkFlow(int source, int sink){
	// flow를 0으로 초기화
	memset(flow, 0, sizeof(flow));

	int totalFlow = 0;

	while(true){
		// BFS로 경로를 찾는다.
		vector<int> parent(MAX_V, -1);
		queue<int> q;

		parent[source] = source;
		q.push(source);
		while(!q.empty() && parent[sink] == -1){
			int here = q.front();
			q.pop();

			for(int there = 0 ; there < V ; there++){
				// 잔여 용량이 남아있는 간선 탐색
				if(capacity[here][there] - flow[here][there] > 0 && parent[there] == -1){
					q.push(there);
					parent[there] = here;
				}
			}
		}

		// 증가 가능한 경로가 없으면 종료
		if(parent[sink] == -1) break;

		// 증가 경로를 통해 얼마나 보낼지 결정
		int amount = INF;
		for(int p = sink ; p != source ; p = parent[p]){
			amount = min(capacity[parent[p]][p] - flow[parent[p]][p], amount);
		}

		// 증가 경로로 유량을 보냄
		for(int p = sink ; p != source ; p = parent[p]){
			flow[parent[p]][p] += amount;
			flow[p][parent[p]] -= amount; // 유량 대칭성
		}

		totalFlow += amount;
	}

	return totalFlow;
}

인접 리스트로 구현할 때에는 유량 대칭성. 즉, 상쇄를 위해 각 정점 사이에 용량이 0인 간선을 추가해줘야 한다. 또한 간선의 반대 방향에 빠르게 접근할 수 있도록 구현해야 한다.

Min-cut Max-Flow Theorem

증가 경로를 잡는 것을 유량 대칭성으로 해결했다고 하였으나 정말 어떤 가능한 어떤 경로를 잡든 항상 최대 유량을 구할 수 있을까? 이를 증명하는 것이 Min-cut Max-Flow Theorem이다.

먼저 개념을 정리하면,

• Cut : Source와 Sink가 서로 다른 집합에 속하도록 정점을 부분 집합으로 나눈 것
• S : Source가 속한 집합
• T : Sink가 속한 집합
• Capacity : 각 집합 (S → T, T → S)로 가는 간선들의 용량 합
• Flow : 각 집합 (S → T, T → S) 로 가는 flow의 합

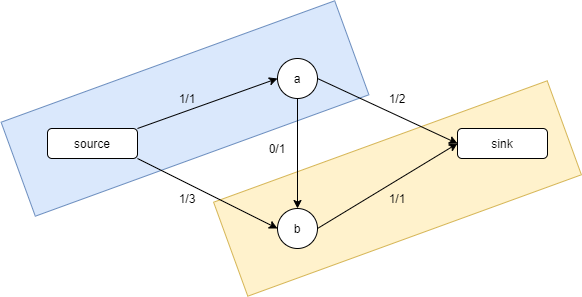
즉 위 예제를 두 개로 나누면 S의 용량은 (1 + 1 + 1) = 3, Flow는 (1 + 1) = 2가 된다.

그리고 이렇게 정의했을 때 다음과 같은 두 속성을 항상 만족한다.

• Cut은 source에서 sink로 가는 총 flow와 같다.
• Cut의 flow는 capacity보다 같거나 작다.

다시말하면, 모든 컷의 유량은 같고 컷의 용량만 다르다는 것인데 여기서 용량이 가장 작은 컷을 찾는 것이 최소 컷 문제라고 부른다. 이 최소 컷 문제는 최대 유량과 밀접한 관련이 있다. 만약 용량과 유량이 같은 S’, T’가 존재한다고 했을 때 S’, T’는 항상 최소 컷임을 만족한다. 만약 S’, T’ 보다 용량이 작은 컷이 존재한다면 유량이 용량보다 크므로 모순이 되고, 더 많은 유량을 내보낼수 있는 방법이 있는 경우 유량이 용량보다 크므로 모순이 된다.

최소 용량 최대 유량 정리는 증가 경로가 존재하지 않는 유량 네트워크에서 용량과 유량이 같은 컷을 찾아내는 방법을 보인다. 먼저 잔여 용량이 존재하는 정점 집합 S와, 그럴 수 없는 정점 집합 T로 나눈다. 여기서 source는 항상 S에 sink는 항상 T에 속하여 컷을 만족하며, S에서 T로 가는 모든 간선의 잔여 용량은 0이 된다. 잔여 용량이 0이라는 것은 모든 간선의 용량과 유량이 같다는 것을 말하므로 찾고자하는 유량과 용량이 같은 컷이 된다. 포드-풀커슨 알고리즘은 유량 네트워크에서 증가 경로가 더 이상 존재하지 않을 때 종료하므로, 이 과정에서 찾은 유량은 네트워크의 최대 유량이 된다.

시간 복잡도

포드-풀커슨의 시간 복잡도는 증가 경로를 몇 번이나 탐색하면 다 찾을 수 있을지 예측하기 어렵기에 구하기가 까다롭다. 첫 번째로는 증가 경로를 하나 찾을 때 마다 유량이 최소 1만큼은 증가한다는 점을 이용해 최대 유량을 f라고 했을 때 그래프 탐색에 드는 비용 $ O(|V| + |E|) $ 를 곱하면 $ O(|E|f) $ 의 시간이 걸린다. 두 번째로는 BFS로 포드-풀커슨을 구현한 에드몬드-카프 알고리즘을 사용했을 때는 증가 경로는 최대 $ O(|V||E|) $ 개로 최대 유량을 구할 수 있음이 이미 증명되어 있다.

따라서 $ O(|E|f) $ , $ O(|V||E|^2) $ 중 작은 것이 시간 복잡도가 된다.

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략