[Algorithm] 오버플로우와 나머지 연산

Modulo 연산

프로그래밍 도중 어떤 값이 int, 그리고 long long의 범위를 초과하여, 그 값을 어떤 수로 나눴을 때의 나머지만을 취할 때가 있다.

모듈러 연산의 분배법칙

1. $ (A+B) \,\bmod\ C = ((A \,\bmod\ C) + (B \,\bmod\ C)) \,\bmod\ C $
2. $ (A-B) \,\bmod\ C = ((A \,\bmod\ C) - (B \,\bmod\ C) + C) \,\bmod\ C $
3. $ (A \times B) \,\bmod\ C = ((A \,\bmod\ C) \times (B \,\bmod\ C)) \,\bmod\ C $

그러나, 이 분배법칙은 나눗셈에 대해서는 성립하지 않는다.

Modulo 연산의 역원

나눗셈에 대한 식을 풀어보면 다음과 같다.
$ (A \div B) \,\bmod\ C = ((A \,\bmod\ C) \times (B^{-1} \,\bmod\ C)) \,\bmod\ C $

$B^{-1}$은 어떻게 구해야할까. 이는 B의 역원을 나타내며 모듈러 연산의 역원은 아래 식을 만족해야 한다.

$ (B \times B^{-1}) \equiv 1\pmod{C} $

모듈러 역원은 존재하지 않을 수 있으며, B와 C가 서로소 일 때만 존재한다.

페르마의 소정리

페르마의 소정리는 다음과 같다.

\[a^{p-1} \equiv 1\pmod{p} \\ (p \quad is \quad prime, \quad a \nmid p)\]

a가 정수이고 p가 소수이며 a가 p의 배수가 아닐 때 위의 식은 항상 성립한다. 이를 이용하면, 나눗셈에 대해 다음과 같은 식을 세울 수 있다.

$ (A \div B) \,\bmod\ C = ((A \,\bmod\ C) \times (B^{C-2} \,\bmod\ C)) \,\bmod\ C $

베주 항등식

페르마의 소정리에서는 나누는 수가 소수일 때만 가능하다는 제약을 가진다. 하지만, 확장 유클리드 알고리즘은 역원을 구하고자 하는 수와 나누는 수가 서로소이기만 하면 사용할 수 있다.

먼저 베주 항등식을 알아야 한다.

\[ax + by = gcd(a,b) \\ 모든 \quad 정수 \quad a, b에 \quad 대해 \quad 이를 \quad 만족시키는 \quad 정수해 \quad x, y가 \quad 존재한다.\]

이를 이용해서 서로소인 B, C를 대입해보면

\[Bx + Cy = gcd(B,C) \\ ((Bx \,\bmod\ C) + (Cy \,\bmod\ C)) \,\bmod\ C = gcd(B,C) \,\bmod\ C \\ Bx \,\bmod\ C = gcd(B,C) \,\bmod\ C = 1\]

이를 이용하면, 나눗셈에 대해 다음과 같은 식을 세울 수 있다.

\[(A \div B) \,\bmod\ C \\ = ((A \,\bmod\ C) \times (B^{-1} \,\bmod\ C)) \,\bmod\ C \\ = ((A \,\bmod\ C) \times (x \,\bmod\ C)) \,\bmod\ C \\\]

위의 부정방정식의 해 x를 도출하기 위한 방법이 확장 유클리드 호제법이다.

확장 유클리드 호제법

확장 알고리즘 전에 유클리드 호제법을 먼저 살펴보도록 한다.

\[a > b, \quad a \equiv r \pmod{b} \quad 이면 \\ gcd(a, b) = gcd(b, r)\]

// a > b
int gcd(int a, int b){
  if(b == 0) return a;
  else return gcd(b, a % b);
}

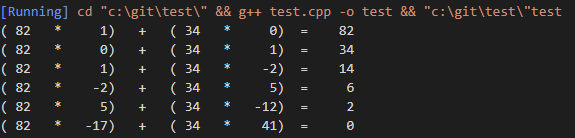
예시로 82, 34의 최대 공약수를 구한다고 해보면 다음과 같다.

\[82 = 34 * 2 + 14 \\ 34 = 14 * 2 + 6 \\ 14 = 6 * 2 + 2 \\ 6 = 2 * 3 + 0 \\ \\ \therefore gcd(82, 34) = 2\]

---

확장 유클리드 호제법은 이러한 계산을 역순으로 한 것과 같다.
먼저 나머지를 기준으로 식을 정리해보면,

\[2 = 14 - 6 * 2 \\ 6 = 34 - 14 * 2 \\ 14 = 82 - 34 * 2 \\\]

해당 식들을 기반으로 다음과 같은 식 전개가 가능하다.

\[gcd(82, 34) = 2 \\ = 14 - (6 * 2) \\ = 14 - (34 - 14 * 2) * 2 \\ = (14 * 5) - (34 * 2) \\ = (82 -34 * 2) * 5 - (34 * 2) \\ = (82 * 5) - (34 * 12) \\ \\ 그러므로, \quad gcd(34, 82) = 82 * x + 34 * y를 \quad 만족시키는 \quad 정수는 \\ x = 5, \quad y = -12\]

---

이제 이를 일반식으로 정리 해보면 유클리브 호제법은 다음과 같은 식을 나타낼 수 있다.

\[a = b * q_0 + r_1 \\ b = r_1 * q_1 + r_2 \\ r_1 = r_2 * q_2 + r_3 \\ ... \\ r_{i-1} = r_i * q_i + r_{i+1}\]

$ r_{i+1} = 0 , r_i = gcd(a, b) $ 가되면 알고리즘이 종료 된다.

여기서, $ r_0 = a , r_1 = b $ 라고 할 때 r을 다음과 같이도 표현할 수 있다.

\[r_0 = 1 * a + 0 * b \\ r_1 = 0 * a + 1 * b \\ ... \\ r_i = s_i * a + t_i * b \\\]

이번에는

\[r_{i-1} = r_i * q_i + r_{i+1} \\ (s_{i-1} * a + t_{i-1} * b) = (s_i * a + t_i * b) * q_i + (s_{i+1} * a + t_{i+1} * b) \\ 적절히 \quad 이항하면 \\ s_{i+1} * a + t_{i+1} * b = (s_{i-1} - s_i * q_i) * a + (t_{i-1} - t_i * q_i) * b \\\] \[\therefore s_{i+1} = s_{i-1} - s_i * q_i, \quad \quad t_{i+1} = t_{i-1} - t_i * q_i\]

#include <cstdio>
#include <vector>

using namespace std;

void extended_gcd(int a, int b);

int main(){
	extended_gcd(82, 34);
}

void extended_gcd(int a, int b){
	vector<int> r = {a, b};
	vector<int> s = {1, 0};
	vector<int> t = {0, 1};
	vector<int> q = {0, 0}; // dummy

	while(r[r.size() - 1] > 0){
		// r1 = r_{i-1}
		int r1 = r[r.size() - 1];
		int r2 = r[r.size() - 2];
		
		q.push_back(r2 / r1);
		r.push_back(r2 % r1);
		
		int s1 = s[s.size() - 1];
		int s2 = s[s.size() - 2];
			
		int t1 = t[t.size() - 1];
		int t2 = t[t.size() - 2];
		
		int q1 = q[q.size() - 1];
		s.push_back(s2 - s1 * q1);
		t.push_back(t2 - t1 * q1);
	}
	
	for(int i = 0 ; i < r.size() ; i++){
		printf("(%3d   *   %3d)   +   (%3d   *   %3d)  =   %3d\n", a, s[i], b, t[i], r[i]);
	}
}