[Algorithm] 크루스칼 알고리즘
Spanning Tree
크루스칼 알고리즘에 대해 알아보기 전에 먼저 스패닝 트리에 대한 개념이 필요하다.
스패닝 트리는 어떤 그래프의 모든 정점과 그래프의 간선들의 부분으로 구성된 ‘부분 그래프’이다.
그러면서 이 부분 집합에 포함된 간선들은 그래프의 모든 정점을 트리 형태로 연결해야한다.
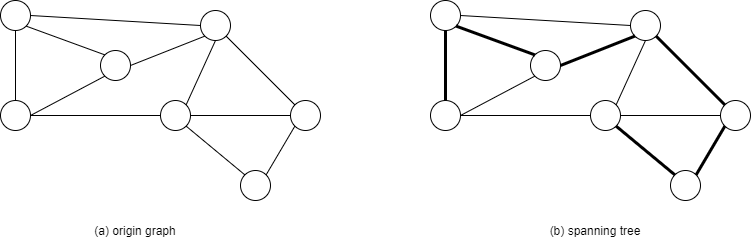
위 그림처럼 그래프 a가 있을 때 b는 a에서 파생된 스패닝 트리이다. 간선들의 집합은 진한 선으로 구성되어 있으며 이는 모든 정점들을 연결한다. 여기서 a의 스패닝 트리는 b뿐만이 아니라 다른 방식으로도 구성할 수 있다. 이 때 만약 그래프가 가중치가 있는 그래프라면 구성할 수 있는 스패닝 트리 중 가중치의 합이 가장 작은 트리를 최소 비용 스패닝 트리 라고 한다.
Kruskal Algorithm
크루스칼 알고리즘은 Greedy algorithm으로 출발한다. 최소 비용으로 스패닝 트리를 구성하기 위해서는 가중치가 높은 간선이 포함되는 것보다, 가중치가 낮은 간선이 포함되는 것이 유리하다.
이 내용을 기반으로 간선의 가중치가 작은 것부터 하나씩 추가해가면서 스패닝 트리를 만들어간다. 과정 중에 사이클이 존재하지 않도록 유지하는 것이 중요하다. 사이클을 생성하는 간선은 추가하지 않는다.
동작 과정 확인

낮은 가중치를 가지는 간선부터 추가한다. 가중치가 12인 간선은 사이클을 생성하므로 선택하지 않는다.
알고리즘의 증명
일반적인 Greedy algorithm을 정당성을 증명하는 방식으로 증명 가능하다.
최소 스패닝 트리를 T라고 하고, 크루스칼 알고리즘으로 구현했을 때 포함되는 간선이 최소 스패닝 트리 T에는 포함되어 있지 않다고 가정한다. 만약 크루스칼 알고리즘이 선택한 간선이 정점 u와 v를 연결한다고 하면, T는 해당 간선이 아닌 다른 어떠한 경로로 u와 v를 연결하고 있다. 이 경로에 포함된 간선 중 하나는 분명히 크루스칼이 선택한 이 간선의 가중치 보다 크다. 그렇지 않으면 해당 경로를 구성하는 간선들이 크루스칼 알고리즘에 의해 이전에 모두 선택되어 이미 u와 v를 연결하는 경로가 존재한다는 모순에 빠진다.
만약 지금 선택된 간선보다 큰 가중치를 가지는 놈을 제거하고 크루스칼이 현재 선택한 간선으로 대체를 한다해도 T가 이미 최소 스패닝 트리이기 때문에 스패닝 트리임을 증명할 수 있다.
코드 구현
struct disjointSet; // disjointSet struct는 직접 구현해야 한다.
const int MAX_V = 100;
int V; // 정점 개수
// 인접 리스트
vector<pair<int, int> > adj[MAX_V];
/*
* @param selected 선택된 엣지 목록 저장
* @return ret MST를 구성하는 가중치의 합
*/
int kruskal(vector<pair<int, int> > & selected){
int ret = 0;
selected.clear();
// (weight, (u, v))
// 가중치 기준으로 검사하기 위해 데이터 손질
vector<pair<int, pair<int, int> > > edges;
for(int u = 0 ; u < V ; u++){
for(int i = 0 ; i < adj[u].size() ; i++){
int v = adj[u][i].first;
int cost = adj[u][i].second;
edges.push_back({cost, {u, v}});
}
}
sort(edges.begin(), edges.end());
// 처음에는 모든 Vertex가 분리
disjointSet sets(V);
for(int i = 0 ; i < edges.size() ; i++){
int cost = edges[i].first;
int u = edges[i].second.first;
int v = edges[i].second.second;
// 사이클을 생성하면 무시
if(sets.find(u) == sets.find(v)) continue;
sets.merge(u, v);
selected.push_back(make_pair(u, v));
ret += cost;
}
return ret;
}
Time Complexity는 Edge들의 정렬인 $ O(|E|log|E|) 가 지배한다.
참고
- 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략
Leave a comment