[Algorithm] 우선순위 큐 & 힙
우선순위 큐
우선순위 큐는 말 그대로 입력 순서가 아닌 원소의 우선순위가 가장 높은 친구가 가장 먼저 꺼내지는 자료구조를 말한다. 이러한 우선순위 큐를 어떻게 구현할까? 단순히 1차원 배열에 다 집어 놓고 순회하여 가장 우선 순위가 높은 원소를 빼는 것은 O(N)의 시간이 소요된다. binary search tree를 사용하여 정렬된 상태로 구성하면 삽입과 삭제가 모두 O(lgN) 시간만에 할 수 있지만 단순히 우선순위가 가장 높은 친구만 찾아내면 되는데 이는 너무 오버 스펙이라고 할 수 있다.
우선순위 큐는 보통 heap을 사용하여 많이 구현한다. 우선순위 큐를 구현하기 위한 heap을 알아보도록 한다.
heap
힙은 아래 규칙을 만족하는 이진 트리이며 최대 값을 가지는 원소를 빠르게 찾아내도록 설계되었다.
- 부모 노드가 가진 원소는 항상 자식 노드가 가진 원소보다 크다
- 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있어야 한다.
- 마지막 레벨에 노드가 있을 때는 항상 가장 왼쪽부터 순서대로 채워져 있어야 한다.
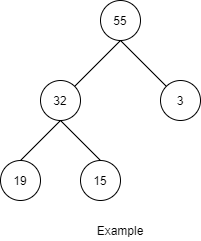
힙의 구현
힙에서 요구하는 빡빡한 조건이 오히려 구현을 쉽게 한다. 노드의 개수만 알고있다면 트리의 구조를 미리 알 수 있기 때문이다.
아래와 같이 힙은 1차원 배열 형태로 구현할 수 있다.
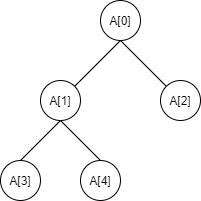
- i번 노드의 왼쪽 자식은 2 * i + 1
- i번 노드의 오른쪽 자식은 2 * i + 2
- i번 노드의 부모는 (i-1) / 2
insert
힙에서의 삽입은 일단 노드를 순서대로 채워야하니 마지막에 삽입한다. 그리고 새 원소를 부모 노드와 비교하고, 부모 노드가 더 작다면 위치를 교환, 부모가 더 작거나 루트에 도달한다면 삽입이 완료된다.
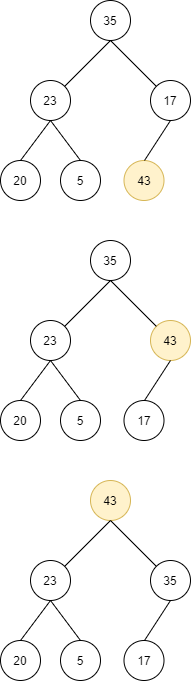
void push_heap(vector<int> & heap, int newValue){
heap.push_back(newValue);
int idx = heap.size() - 1;
while(idx > 0 && heap[(idx-1) / 2] < heap[idx]){
swap(heap[idx], heap[(idx-1) / 2]);
idx = (idx - 1) / 2;
}
}
POP
힙에서 값을 꺼내는 연산이다. 가장 우선순위가 높은 root가 제거되고, 다시 자리 잡은 모양은 마지막 노드가 사라진 모양이다. 일단 마지막 노드를 root로 올린 다음에 제자리를 찾아가는 식으로 구현하면 된다. 두 자식 노드 중 더 큰 값을 가지는 노드를 다시 올리고, 이를 두 자식 모두 값이 작거나 또는 바닥까지 도달하거나 하면 삭제가 완료된다.
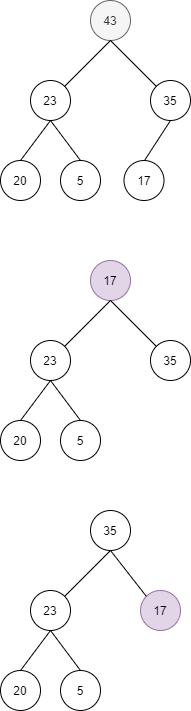
void pop_heap(vector<int> & heap){
heap[0] = heap.back();
heap.pop_back();
int here = 0;
while(true){
int left = here * 2 + 1;
int right = here * 2 + 2;
if(left >= heap.size()) break;
int next = here;
if(heap[next] < heap[left]) next = left;
if(right < heap.size() && heap[next] < heap[right]) next = right;
if(next == here) break;
swap(heap[here], heap[next]);
here = next;
}
}
참고
- 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략
Leave a comment