[Algorithm] Graph

Graph의 정의

그래프는 현실 세계의 사물이나 추상적인 개념 간의 연결 관계를 표현합니다.
그래프 G(V, E)는 어떤 자료나 개념을 표현하는 Vertex의 집합 V, 이들을 연결하는 Edge의 집합 E로 구성된 자료 구조입니다.

Graph의 종류

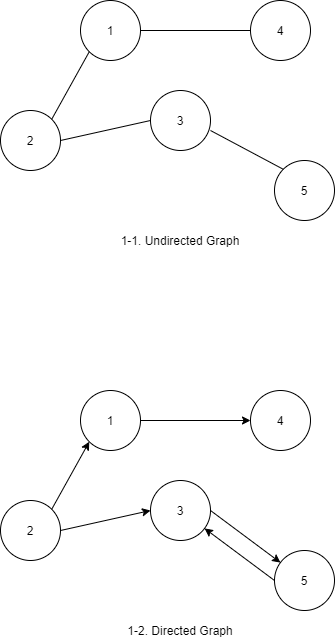
1. Undirected Graph와 Directed Graph

   무향 그래프는 방향이 없으며, 방향이 있는 유향 그래프에서는 ‘방향’이라는 추가 속성을 가진다.

   

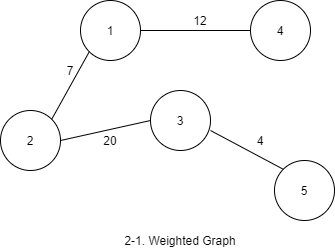
2. Weighted Graph

   가중치 그래프는 각 엣지에 가중치가 존재한다. 도시 사이의 거리 등의 정보를 표기할 수 있다.

   

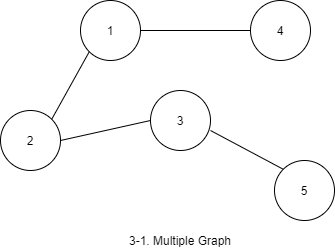
3. Multiple Graph

   다중 그래프는 정점 사이의 연결이 여러 개가 될 수 있다.

   

이 외에도 다양한 종류의 그래프를 정의할 수 있다.

Path

경로는 정점 사이의 이동을 나타낸다.

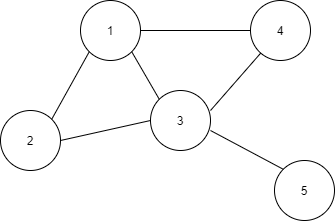
3번에서 출발하여 1번으로 도착할 때, 경로는 3 -> 1이 될 수 있다. 뭐 어떤 식으로 도착해도 상관 없다고 하면 3 -> 1 -> 4 -> 3 -> 1으로도 갈 수 있다.

하지만 그래프 이론에서 일반적으로 말하는 경로는 같은 정점을 중복해서 방문하지 않는 Simple Path를 말한다. 한 정점을 두 번 이상 방문하는 경우에는 별도로 이 사실을 명시해준다.

Graph의 표현

1. Adjacency List(인접 리스트)

   adjacency list는 그래프의 각 정점마다 해당 정점에서 나가는 엣지의 목록을 저장한다.

    // adjacent[i]는 정점 i에서 연결된 정점의 번호들을 저장한다.
    vector<list<int> > adjacent;
   
    // weight와 같은 추가 속성들을 정의할 때는 별도로 정의해서 구현하면 된다.
    struct Edge{
        int vertex;
        int weight;
    }
    vector<list<struct Edge>> adjacent;
   

2. Adjacency Matrix(인접 행렬)

   adjacency matrix는 2차원 배열으로 나타낸다.

    // adjacent[i][j]는 정점 i와 정점 j의 연결 여부를 나타낸다.
    vector<vector<bool> > adjacent;
   
    // weight와 같은 추가 속성 표현도 좀 더 직관적으로 할 수 있다.
    // adjacent[i][j] 값이 가중치를 나타내고, 연결되지 않음은 -1 등으로 표현하면 된다.
    vector<vector<int> > adjacent;
   

	Adjacency Graph	Adjacency List
정점 연결 여부 확인	adjacent[i] 리스트 순회	adjacent[i][j]로 바로 접근
Space Complexity	$ O(|V| + |E|) $	$ O(|V|^2) $
적합한 표현	Sparse Matrix	Dense graph

대다수의 경우에는 $ |V|^2 $ 로 표현하는데 무리가 없다. 하지만 간선 수에 비해 정점 수가 훨씬 많은 sparse matrix는 인접 리스트 형태로 표현하는게 적합하다.

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략