[Algorithm] 다익스트라 알고리즘
다익스트라(dijkstra) 알고리즘
다익스트라 알고리즘은 가중치가 있는 그래프에서 특정 노드에서 다른 노드에 도착하는데 필요한 최소 거리를 구하는 알고리즘이다.
가중치는 양수의 값만 고려한다. 만약 음수의 가중치가 존재하는 경우는 벨만-포드 알고리즘을 고려한다.
다익스트라의 구현은 BFS를 통한 최단거리를 찾는 것과 유사한 구조를 가진다. BFS는 그래프에서 가중치가 없기 때문에 큐를 통해서 삽입하고 순서대로 방문한다. 반면, 다익스트라에서는 가중치를 포함하여 우선순위 큐에 삽입하고 가장 짧은 가중치를 가진 정점을 순서대로 방문하는 컨셉이다.
각 정점까지의 최단 거리를 저장할 배열 dist[]를 유지하며, 정점을 방문할 때마다 인접한 모든 정점을 검사한다.
간선 (u, v)를 검사했는데 v가 만약 방문하지 않은 정점이라고 하자.
먼저 시작점에서 u까지의 최단 거리에서 (u ,v)를 더해 v까지의 거리를 찾는다.
만약 이 값이 저장된 dist[u] 보다 작다면 값을 갱신하고 (dist[v], v)를 큐에 삽입한다.
구현
#define INF 99999999
// 정점의 개수
int vertexCnt = 10;
// 그래프 인접 리스트
vector<pair<int, int> > adj[vertexCnt];
vector<int> dijkstra(int startV){
vector<int> dist(vertextCnt, INF);
dist[startV] = 0;
priority_queue<pair<int, int> > pq;
pq.push(make_pair(0, startV));
while(!pq.empty()){
int cost = -pq.top().first; // 기본 pq는 가장 큰 값이 우선 순위가 제일 높으므로 부호로 음수로 삽입을 하여 절대값이 작은 것부터 뽑음
int curPos = pq.top().second;
pq.pop();
// 만약 지금 꺼낸 것보다 더 짧은 경로를 알고 있다면 무시한다.
if(dist[curPos] < cost) continue;
for(int i = 0 ; i < adj[curPos].size() ; i++){
int to = adj[curPos][i].first;
int viaCost = cost + adj[curPos][i].second;
// 더 짧은 경로를 발견하면 dist를 갱신하고 큐에 삽입한다.
if(viaCost < dist[to]){
dist[to] = viaCost;
pq.push(make_pair(-dist[to], to)); // pq 우선순위 때문에 음수 값 삽입
}
}
}
return dist;
}
동작 과정 확인
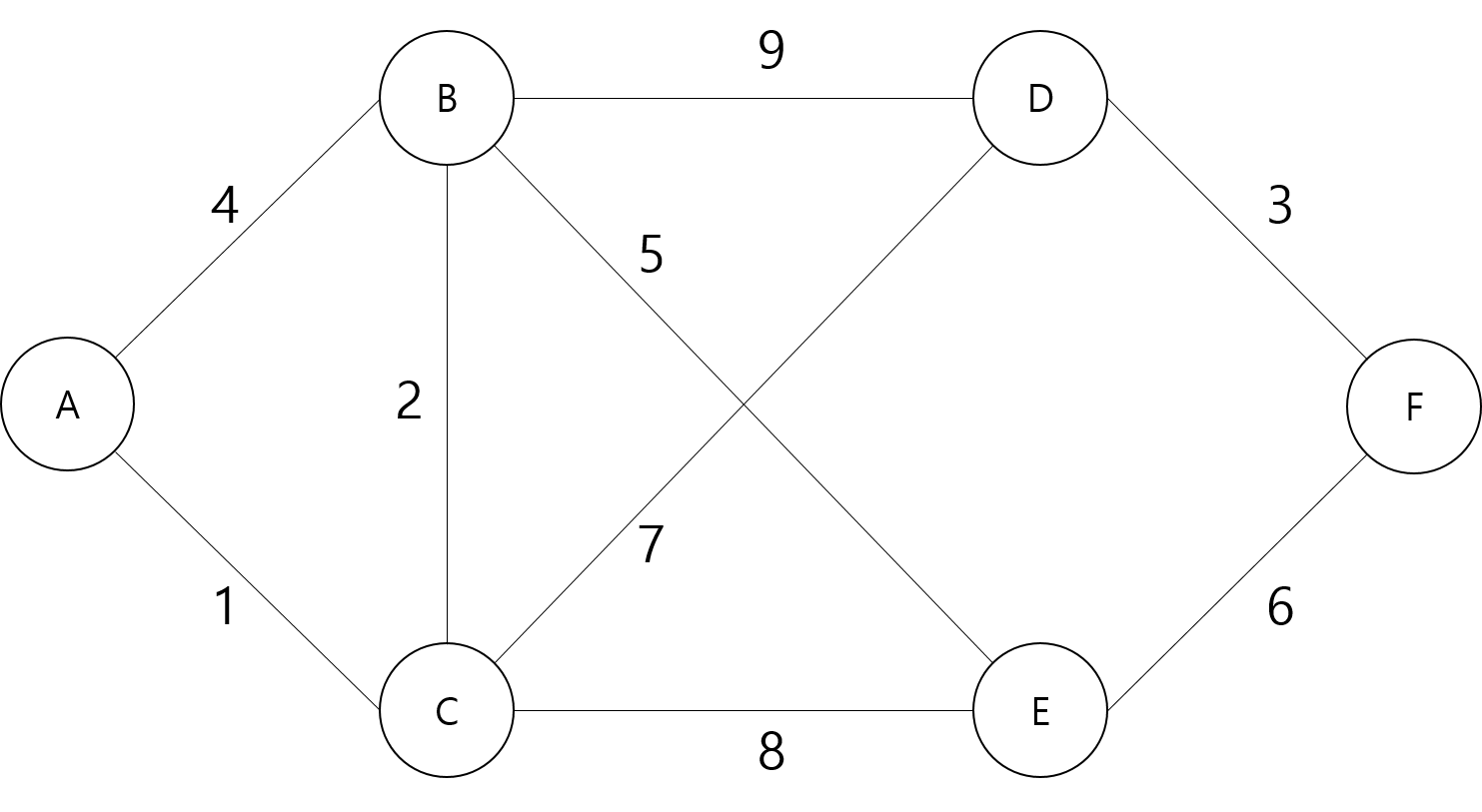
해당 가중치를 2차원 배열로 나타내면 다음과 같다
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 4 | 1 | ∞ | ∞ | ∞ |
| B | 4 | 0 | 2 | 9 | 5 | ∞ |
| C | 1 | 2 | 0 | 7 | 8 | ∞ |
| D | ∞ | 9 | 8 | 0 | ∞ | 3 |
| E | ∞ | 5 | 8 | ∞ | 0 | 6 |
| F | ∞ | ∞ | ∞ | 3 | 6 | 0 |
Vertex A에서 출발한다고 가정하자. 먼저 A에서의 초기 비용은 다음과 같다.
방문한 곳 : A
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 4 | 1 | ∞ | ∞ | ∞ |
여기서, 최소 비용을 가지는 곳은 C이고 이를 거쳐서 가는 것을 기준으로 값을 다시 셋팅한다.
방문한 곳 : A, C
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 3 | 1 | 8 | 9 | ∞ |
이후, 최소 비용을 가지는 곳은 B이다.
방문한 곳 : A, C, B
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 3 | 1 | 8 | 8 | ∞ |
방문한 곳 : A, C, B, D
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 3 | 1 | 8 | 8 | 14 |
방문한 곳 : A, C, B, D, E
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 3 | 1 | 8 | 8 | 11 |
방문한 곳 : A, C, B, D, E, F
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 3 | 1 | 8 | 8 | 11 |
위 시뮬레이션을, 소스로 나타내면 아래와 같다.
#define INF 99999999
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
void infoInit();
vector<int> dijkstra(int);
int V = 6;
vector<pair<int, int> > disInfo[6]; // 간선 정보
int main(){
infoInit();
vector<int> dist = dijkstra(0);
// for(int i = 0 ; i < 6 ; i++) {cout << dist[i] << " ";}
cout << "\n";
}
void infoInit(){
// 0(A) -> 1(B) : 4(weight)
disInfo[0].push_back(make_pair(1, 4));
disInfo[0].push_back(make_pair(2, 1));
disInfo[1].push_back(make_pair(0, 4));
disInfo[1].push_back(make_pair(2, 2));
disInfo[1].push_back(make_pair(3, 9));
disInfo[1].push_back(make_pair(4, 5));
disInfo[2].push_back(make_pair(0, 1));
disInfo[2].push_back(make_pair(1, 2));
disInfo[2].push_back(make_pair(3, 7));
disInfo[2].push_back(make_pair(4, 8));
disInfo[3].push_back(make_pair(1, 9));
disInfo[3].push_back(make_pair(2, 7));
disInfo[3].push_back(make_pair(5, 3));
disInfo[4].push_back(make_pair(2, 8));
disInfo[4].push_back(make_pair(1, 5));
disInfo[4].push_back(make_pair(5, 6));
disInfo[5].push_back(make_pair(3, 3));
disInfo[5].push_back(make_pair(4, 6));
}
vector<int> dijkstra(int startV){
vector<int> dist(V, INF);
dist[startV] = 0;
priority_queue<pair<int, int> > pq;
pq.push(make_pair(0, startV));
while(!pq.empty()){
int cost = -pq.top().first; // 기본 pq는 가장 큰 값이 우선 순위가 제일 높으므로 부호로 음수로 삽입을 하여 절대값이 작은 것부터 뽑음
int curPos = pq.top().second;
pq.pop();
if(dist[curPos] < cost) continue;
for(int i = 0 ; i < disInfo[curPos].size() ; i++){
int to = disInfo[curPos][i].first;
int viaCost = cost + disInfo[curPos][i].second;
if(viaCost < dist[to]){
dist[to] = viaCost;
pq.push(make_pair(-dist[to], to)); // pq 우선순위 때문에 음수 값 삽입
}
}
}
return dist;
}
시간 복잡도
우선순위의 큐가 가장 커지는 최악의 시나리오는 그래프의 모든 간선이 검사될 때마다 dist가 갱신되고 우선순위 큐에 정점이 추가되는 것이다. 삽입은 간선마다 최대 한 번이기 때문에 원소의 수는 최대 $ O(|E|) $ 가 된다.
그리고 이 때 추가, 삽입에 걸리는 시간은 $ O(lg|E|) $ 이므로, $ O(|E|) $ 개의 원소에 대한 처리는 $ O(|E|lg|E|) $ 가 된다. 이 때 대개의 그래프에서 $ |E| $ 는 $ |V|^2 $ 보다 작기 때문에, $ O(|E|lg|V|) $ 로 표현할 수도 있다.
참고
- 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략
Leave a comment