[Algorithm] 이분 매칭

Bipartite Matching

매칭

N명의 학생이 소풍을 가는데, 단독 행동을 막기 위해서 두 명씩 짝을 이루려고 한다. 하지만 사이가 나쁜 학생들 끼리 짝을 지으면 문제가 발생할 수 있기에 서로 사이가 좋은 학생끼리만 짝을 짓고자 한다. 이 때 모든 학생이 짝을 지을 수 있는지, 아니라면 최대 몇 쌍이나 짝을 지어줄 수 있는가?

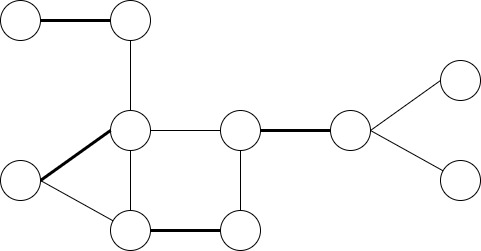
위 문제는 그래프로 간단하게 표현할 수 있다. 학생들을 정점으로 나타내고 친한 학생들 끼리 간선으로 연결한다. 그리고 실제 매칭된 학생들의 짝을 굵은 실선으로 표현하면 이들 간선은 정점들을 서로 공유하지 않는 집합이 된다.

이러한 간선의 집합을 그래프의 Matching이라고 한다.

이분 매칭

매칭 문제 중에서도 이분 매칭이 현실 세계의 문제와 직관적으로 잘 대응된다. 전형적인 예시로 N명의 사람들에게 N개의 작업을 배정할 때 각 사람이 할 수 있는 작업은 정해져 있다고 가정하자. 이는 이분 그래프로 두 집합 간의 대응 관계를 나타낼 수 있다.

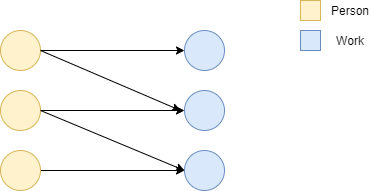
이분 매칭은 네트워크 플로우를 사용하여 해결할 수 있다. 왼쪽의 작업자들 그룹 A, 오른쪽의 작업을 그룹 B라고 했을 때, A에 source를 추가하고, B에 sink를 추가하여 flow network를 만든다. 그리고 이 때 모든 간선의 용량은 1로 설정한다.

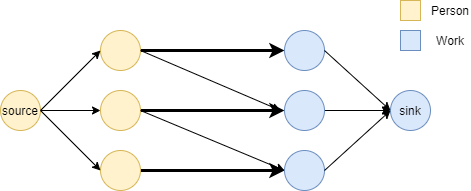
그리고 그래프의 최대 유량을 구한다. 최대 유량을 구했을 때 유량이 발생하는 간선들을 모으면 그것이 최대 매칭이 된다.

이 경우 네트워크의 최대 유량이 $ O(|V|) $ 이므로, 포드-풀커슨 시간복잡도를 따르면 $ O(|E|f) = O(|V||E|) $가 된다.

이분 매칭 구현

포드-풀커슨 알고리즘으로도 해결 가능하지만 이분 그래프의 특성으로 좀 더 간단한 알고리즘 구성이 가능하다.

#define MAX_N 30
#define MAX_M 30

#include <iostream>
#include <vector>

using namespace std;

// Group A, Group B 정점의 개수
int n, m;

// A_i와 B_i의 연결 여부
bool adj[MAX_N][MAX_M];

// 각 정점에 매칭된 상대 정점 번호 저장
vector<int> aMatch, bMatch;

// dfs 방문 여부
vector<bool> visited;

bool dfs(int a);
int bipartiteMatch();

int main(){
	n = 3;
	m = 3;

	adj[0][0] = true;
	adj[0][1] = true;

	adj[1][1] = true;
	adj[1][2] = true;

	adj[2][2] = true;

	int size = bipartiteMatch();
	cout << size << endl;

	return 0;
}

bool dfs(int a){
	if(visited[a]) return false;
	visited[a] = true;
	
	for(int b = 0 ; b < m ; b++){
		if(adj[a][b]){
			// b가 이미 매칭되어 있으면 bMatch[b]에서 부터 시작해 증가 경로를 찾음
			if(bMatch[b] == -1 || dfs(bMatch[b])){
				// 증가 경로 발견
				aMatch[a] = b;
				bMatch[b] = a;

				return true;
			}
		}
	}

	return false;
}

int bipartiteMatch(){
	// 초기화
	aMatch = vector<int>(n, -1);
	bMatch = vector<int>(m, -1);

	int size = 0;

	for(int start = 0 ; start < n ; start++){
		visited = vector<bool>(n, false);

		// dfs를 사용해 start에서 시작하는 증가 경로를 찾음
		if(dfs(start)) size++;
	}

	return size;
}

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략