[Algorithm] 벨만-포드 알고리즘

벨만-포드(Bellman-Ford) 알고리즘

벨만-포드 알고리즘은 다익스트라 알고리즘과 같이 특정 정점에서 다른 정점으로의 최소 거리를 구하는 알고리즘이다. 그러나, 벨만-포드 알고리즘은 음수 간선이 존재하는 그래프에 대해서도 최단 경로를 찾을 수 있으며, 음수 사이클이 존재해 최단 거리가 정의되지 않을 때도 구분할 수 있다.

시작점에서 각 정점까지 가는 최단 거리의 상한선을 적당히 예측한 뒤 예측 값과 실제 최단 거리 사이의 오차를 반복적으로 줄여가는 방식으로 동작한다.

각 정점까지의 최단거리를 담은 upper[]를 유지하며, 출발점을 제외한 모든 노드까지의 거리를 무한대로 초기화 하고, 아래 특성을 이용해 값을 갱신해간다.

시작점에서 v, u까지의 거리를 dist[v], dist[u] 라고 할 때 항상 아래 성질을 만족한다.

\[dist[v] \leq dist[u] + w(u, v)\]

당연히 dist[]를 최단거리로 정의했으니 u를 경유해서 갔을 때 더 짧다는 것은 전제에 모순된다. 이러한 성질을 가지고 계속해서 upper[]를 보정한다.

보정 결과가 upper[]와 dist[]가 같다고 보장할 수 있을까?

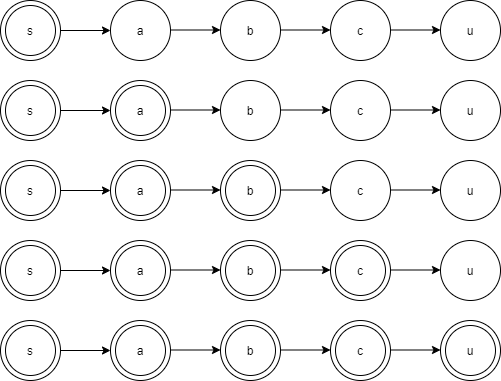
시작점 s에서 정점 u까지의 최단 거리를 위 그림이라고 하고, 위 그림은 최단 거리가 보장된 정점은 동심원으로 표현한다.

$ upper[a] \leq upper[s] + w(s, a) $ 가 성립하고, 시작점 s에 대한 upper[s]의 값은 0이기 때문에 $ upper[a] \leq w(s, a) $ 가 성립한다. 이 때, w(s, a)는 dist[a]가 보장된다. 이게 최단 거리가 아니라면 애초에 (s-a-b-c-u)가 최단 거리라는 전제와 모순이기 때문이다.

이 과정을 반복하면 차례대로 최단 거리를 구할 수 있고 네 번 진행하면 $ upper[s] = dist[s] $ 를 구할 수 있다. 이렇게, |V| - 1 번 반복하면 모든 간선에 대한 최단 거리를 구할 수 있다.

음수 사이클 판정

일반적인 그래프를 확인할 때는 |V| - 1 번 반복하면 모든 최단 거리를 구할 수 있다. 그런데 만약 음수 사이클이 존재한다면 |V| 번 이상에 대한 완화 작업에도 완화가 성공한다.
이러한 점을 이용해서 |V|번 반복하여 최단 거리 및 음수 사이클의 존재 여부를 확인할 수 있다.

구현

#define INF 99999999

// 정점의 개수
int V;
// 인접 리스트 (연결된 정점 번호, 간선 가중치)
vector<pair<int, int> > adj[MAX_V];

// 음수 사이클이 존재할 때는 빈 배열 반환
vector<int> bellmanFord(int startV){
	vector<int> upper(V, INF);
	upper[startV] = 0;
	bool updated;

	for(int iter = 0 ; iter < V ; ++iter){
		updated = false;
		for(int here = 0 ; here < V ; ++here){
			for(int i = 0 ; i < adj[here].size() ; i++){
				int there = adj[here][i].first;
				int cost = adj[here][i].second;

				// upper 보정
				if(upper[there] > upper[here] + cost){
					upper[there] = upper[here] + cost;
					updated = true;
				}
			}
		}

		if(!updated) break;
	}
	
	// V번째 순회에서도 완화가 성공했으면, 음수 사이클이 존재한다.
	if(updated) upper.clear();
	return upper;
}

주의해야 할 점

만약 특정 정점으로의 경로가 있는지 확인하기 위해서는 upper[] 값이 최초 정의한 INF 와 비교해본다고 생각하기 쉽다.

하지만 음수의 가중치가 존재한다면 INF 값이 자꾸 완화된다. 따라서 특정 정점으로 가는 경로가 존재함을 확인하기 위해서는 적당히 큰 값 M을 정의하여 $ upper[u] < \infty - M $ 인지 확인해야 한다.

시간 복잡도

가장 바깥의 for문은 정점의 개수인 V만큼, 안 쪽의 이중 for문은 모든 간선의 수인 E만큼 순회하므로 시간 복잡도는 $ O(|V||E|) $ 이다.

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략